Recently, I’ve come across Jane Street’s archive of puzzles; ranging from riddles, math, chess, and other quantitative problems. These have been challenging to say the least, but a lot of fun to figure out. Jane Street is a proprietary trading firm that engages in market making and arbitrage. I figured that these puzzles would give me a good idea as to how the minds at Jane Street think when they are problem solving and developing solutions for their business.
After searching the archives, I found a puzzle from June 2019 that I felt would be interesting to try to figure out. Titled “Hooks #5”, it is a math and numbers based puzzle. I’ve attached the prompt in the picture below…
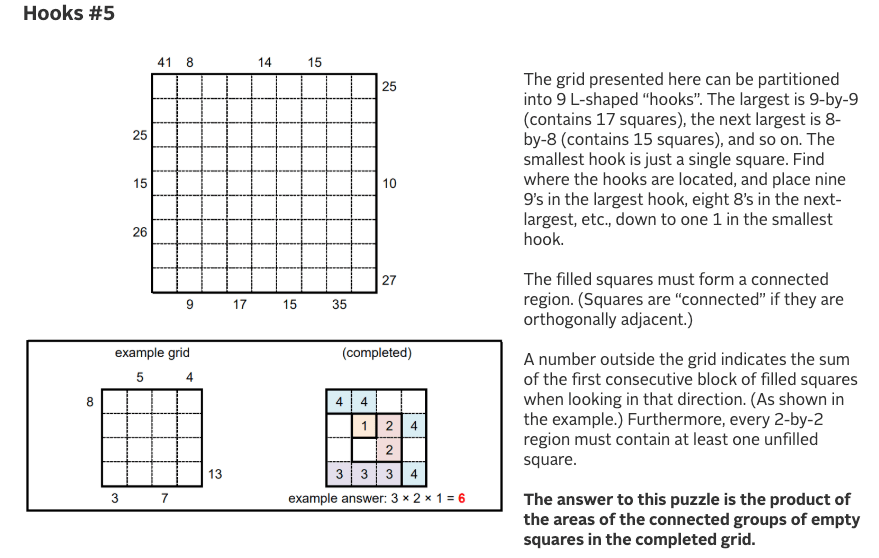
Although it was tough to grasp the rules after reading it the first time, I broke it down to make it easier for myself. Essentially, there are 9 sets of hooks starting with a 9 block hook going down all the way to 1 that must be strategically placed to complete the 9×9 box grid. Squares that are part of the hook must be “orthogonally adjacent”, which just means that the sides have to touch. Along the outside of the box grid there are numbers which are meant to indicate the sum of the first set of consecutive blocks looking from that direction’s perspective as a tool to get you started. After the grid is filled, the answer can be found by finding the product of the area of the empty grids (multiplying the groups of connected empty grids with each other). Once I understood the rules, I felt confident enough to get started.
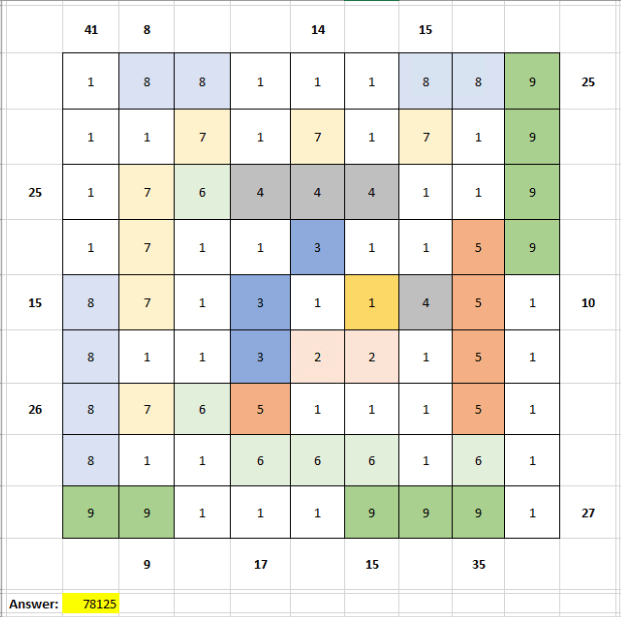
It has become a habit of mine to use excel for almost everything because I see it as a basic programming language that has a lot of different tools and resources that make working with numbers more efficient. Being that this was a grid-based puzzle, it only made sense for me to use excel. After setting up the grid like how it was displayed on the prompt, I began filling in the squares, using the numbers on the outside as a guide. There were a lot of different combinations that would add up to make the outside numbers, so it was a lot of trial-and-error, but also logical. The first few sets of hooks, from 9 to 7, came to me quick. The deeper I got within the grid however, the more I had to experiment with number combinations, but they made sense keeping in mind that they had to be orthogonally adjacent.
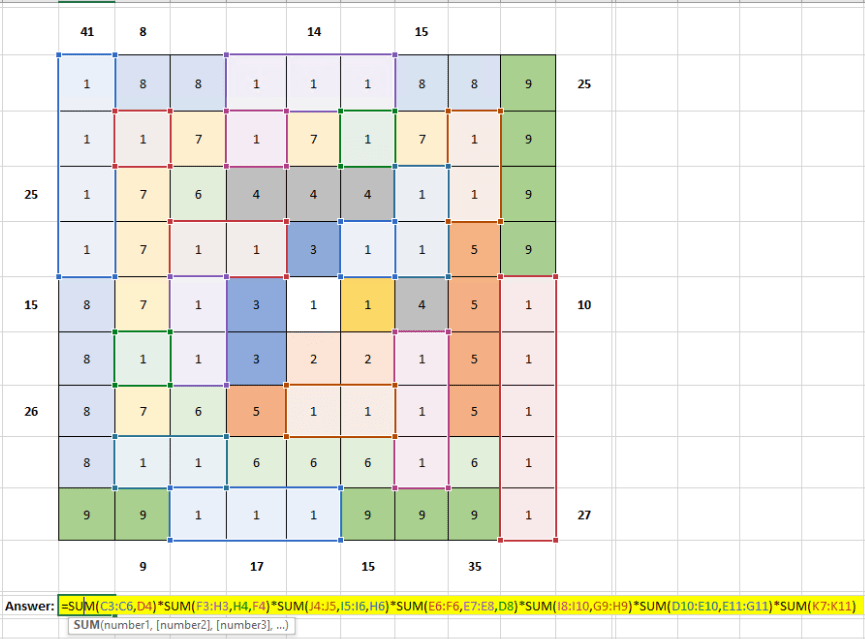
By color coding each set of hooks, I was able to follow my work easier than if I were to have done it on paper. This also allowed me to place 1’s in all of the empty regions so that once the grid was filled, I could simply get the sum of each region and multiply them together (as shown in the screenshot above). I found that by using this method, I could get the most accurate answer and avoid any miscounting or math errors. This gave my answer to the puzzle, which was 78125.
It took me about a weekend’s worth of analyzing and working on the puzzle to get to my answer. What I enjoy most about these puzzles are that they really make you sit there and think critically. You have to break them down before you even start your attempt, and that challenge is what makes it fulfilling once you finish. It builds good habits that can carry over into any type of problem solving scenario outside of these puzzles. I’ll keep my eyes out for new puzzles while I try to work out some of the older ones. I’ve added a link to Jane Street’s puzzle page for anyone who want to try them as well (https://www.janestreet.com/puzzles/archive/).
-S.F.
